A Java Implementation of Dijkstra's Algorithm
A Java Implementation of Dijkstra’s Algorithm
In this article I’d like to show you a java implementation of Dijkstra’s Algorithm I’ve written.
I’m reading the book Grokking Algorithm1 recently, and it introduces Dijkstra’s Algorithm in chapter 7. Here is a java implementation I’ve written:
import java.util.*;
/**
* Created by weli on 26/02/2017.
*/
public class Graph {
class Edge {
private String from;
private String to;
private int weight;
public String getFrom() {
return from;
}
public String getTo() {
return to;
}
public int getWeight() {
return weight;
}
public Edge(String from, String to, int weight) {
this.from = from;
this.to = to;
this.weight = weight;
}
@Override
public String toString() {
return "{" + from + "->" + to + " / " + weight + "}";
}
}
private List<Edge> edges = new ArrayList<>();
private Set<String> nodes = new HashSet<>();
private Map<String, String> path = new HashMap<>(); // to -> from
private Map<String, Integer> costs = new HashMap<>();
private List<String> processed = new ArrayList<>();
private String start = "start";
private String fin = "fin";
{
processed.add(start);
processed.add(fin);
}
public String getStart() {
return start;
}
public String getFin() {
return fin;
}
public void addEdge(String from, String to, int weight) {
edges.add(new Edge(from, to, weight));
nodes.add(from);
nodes.add(to);
if (from.equals(start)) {
costs.put(to, weight);
} else if (costs.get(to) == null) {
costs.put(to, Integer.MAX_VALUE);
}
}
private String nextCheapestNode() {
if (nodes.size() == processed.size()) // all nodes are processed
return null;
int cheapest = Integer.MAX_VALUE;
String cheapestNode = null;
for (Map.Entry<String, Integer> cost : costs.entrySet()) {
System.out.println("Updated cost:" + cost);
if (cost.getValue() <= cheapest && !processed.contains(cost.getKey())) {
cheapest = cost.getValue();
cheapestNode = cost.getKey();
}
}
System.out.println("next cheapest: " + cheapestNode);
return cheapestNode;
}
public void dijkstra() {
System.out.println("Initial costs: " + costs);
String node = nextCheapestNode();
path.put(node, start);
while (node != null) {
int cost = costs.get(node);
Set<Edge> neighbors = findNeighbors(node);
for (Edge neighbor : neighbors) {
int newCost = cost + neighbor.getWeight();
if (costs.get(neighbor.getTo()) > newCost) {
costs.put(neighbor.getTo(), newCost);
path.put(neighbor.getTo(), neighbor.getFrom());
}
}
processed.add(node);
node = nextCheapestNode();
}
}
private String generatePath() {
StringBuffer result = new StringBuffer();
String next = null;
for (Map.Entry<String, String> p : path.entrySet()) {
if (p.getKey().equals(fin)) {
result.append(p.getKey()).append(" <- ");
next = p.getValue();
}
}
while (next != null) {
for (Map.Entry<String, String> p : path.entrySet()) {
if (p.getKey().equals(next)) {
result.append(p.getKey()).append(" <- ");
next = p.getValue();
if (next.equals(start)) {
result.append(start);
next = null;
}
}
}
}
return result.toString();
}
private Set<Edge> findNeighbors(String node) {
Set<Edge> neighbors = new HashSet<>();
for (Edge edge : edges) {
if (edge.getFrom().equals(node)) {
neighbors.add(edge);
}
}
return neighbors;
}
@Override
public String toString() {
return "Graph{" +
"edges=" + edges +
'}';
}
public Map<String, String> getPath() {
return path;
}
public static void main(String[] args) throws Exception {
Graph g = new Graph();
g.addEdge("start", "a", 1);
g.addEdge("start", "b", 1);
g.addEdge("a", "b", 1);
g.addEdge("b", "c", 1);
g.addEdge("a", "c", 1);
g.addEdge("c", "fin", 1);
g.addEdge("b", "fin", 1);
System.out.println(g);
g.dijkstra();
System.out.println(g.getPath());
System.out.println(g.generatePath());
}
}
I’ll introduce the above implementation in this article. Firstly, the usage is like this:
public static void main(String[] args) throws Exception {
Graph g = new Graph();
g.addEdge("start", "a", 1);
g.addEdge("start", "b", 1);
g.addEdge("a", "b", 1);
g.addEdge("b", "c", 1);
g.addEdge("a", "c", 1);
g.addEdge("c", "fin", 1);
g.addEdge("b", "fin", 1);
System.out.println(g);
g.dijkstra();
System.out.println(g.getPath());
System.out.println(g.generatePath());
}
The above code created a Graph class, and added edges into the graph, and then the dijkstra() method is executed to calculate the cheapest path. Here is the execution result:
Graph{edges=[{start->a / 1}, {start->b / 1}, {a->b / 1}, {b->c / 1}, {a->c / 1}, {c->fin / 1}, {b->fin / 1}]}
Initial costs: {a=1, b=1, c=2147483647, fin=2147483647}
Updated cost:a=1
Updated cost:b=1
Updated cost:c=2147483647
Updated cost:fin=2147483647
next cheapest: b
Updated cost:a=1
Updated cost:b=1
Updated cost:c=2
Updated cost:fin=2
next cheapest: a
Updated cost:a=1
Updated cost:b=1
Updated cost:c=2
Updated cost:fin=2
next cheapest: c
{b=start, c=b, fin=b}
fin <- b <- start
We can see how the path costs are updated in each iteration, and how the final path is calculated at last. Here is the class diagram:
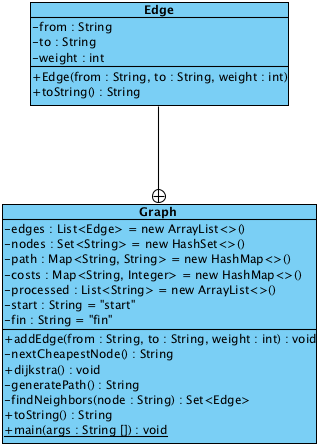
The Graph class is to store the structure DAG, of which the full name is Directed Acyclic Graph. The Graph contains a lot of edges, so the Edge class is to represent the structure.
Here are the attributes in Edge class:
class Edge {
private String from;
private String to;
private int weight;
}
from and to are two nodes of connected by the edge. We use String as node class. This is okay because we don’t allow different nodes to have same name. The weight attribute is straight-forward and it stores the weight of this edge for calculation. Because Graph contains many edges, so in Graph class, we store these edges like this:
private List<Edge> edges = new ArrayList<>();
We also need to store all the nodes in graph for later calculation:
private Set<String> nodes = new HashSet<>();
Please note we use Set<String> to store the nodes, because Set type will not store entries with same value. This can ensure no duplicated nodes will appear in the data structure. The next important data structure is the cost table:
private Map<String, Integer> costs = new HashMap<>();
This table stores the weight sum from the start point to the target node. During calculation process, this table will be keep updated.
Another important thing is that we use Map<String, Integer> type to store the node <-> weight sum pair,because the Map type is simliar to the Set type, it won’t accept duplicate key value, which means it won’t contain multiple entries for same node.
If we put a String <-> Integer pair with an existing String value in Map, it will just update the existing entry. That is just what we need: to update the node <-> weight sum entry with new value.
We also need to mark the start node and the end node of a graph, and here are the relative attributes in Graph class:
private String start = "start";
private String fin = "fin";
We can compare the node name in calculation process to check if it is start or end point. Now let us check the methods in Graph:
public void addEdge(String from, String to, int weight) {
edges.add(new Edge(from, to, weight));
nodes.add(from);
nodes.add(to);
if (from.equals(start)) {
costs.put(to, weight);
} else if (costs.get(to) == null) {
costs.put(to, Integer.MAX_VALUE);
}
}
The purpose of above method is to add an edge into graph:
edges.add(new Edge(from, to, weight));
And also add the two nodes of the edge into nodes set:
nodes.add(from);
nodes.add(to);
We do not need to worry that we will add duplicate nodes into nodes set, because the type of nodes is Set, it does not contain duplicate entries with same value. Adding the String with same value will just overwrite the existing one. The next important task of addEdge is to update the costs table:
if (from.equals(start)) {
costs.put(to, weight);
} else if (costs.get(to) == null) {
costs.put(to, Integer.MAX_VALUE);
}
We need to consider two conditions as shown above: Firstly, we need to check if the added edge is connected with start point. If so, we need to save the true weight into costs table, because they are initial edges need to be calculated by the algorithm.
Otherwise, we just use Integer.MAX_VALUE as the weight of the edge, because we do not want the algorithm to pick up these edges in initial calculation. During the calculation process, the true costs of these edges can be fetched from the weight attribute of Edge class later for calculation. Please note this condition:
else if (costs.get(to) == null)
We need to check whether costs table contains the to node of the added edge, in case the weight value is overwrittee. This is important because the node connecting with start node may be part of multiple edges, and the edge that is not connecting with start node may overwrite the weight value of this node. Here is the diagram for example:
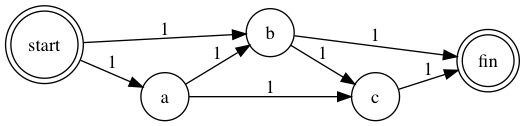
As the diagram shown above, b is connected with both start and c, so it belongs to two edges: start -> b and b -> c. In this case, if we add edge start -> b firstly, the cost of b will be 1 in costs table.
But if we add edge b -> c later, the cost of b will be updated with value Integer.MAX_VALUE if we don’t check the existing value in costs table, and then the algorithm will fail because the initial weight of b, which is connected with start node, is not correct. Now let’s see nextCheapestNode() method:
private String nextCheapestNode() {
if (nodes.size() == processed.size()) // all nodes are processed
return null;
int cheapest = Integer.MAX_VALUE;
String cheapestNode = null;
for (Map.Entry<String, Integer> cost : costs.entrySet()) {
System.out.println("Updated cost:" + cost);
if (cost.getValue() <= cheapest && !processed.contains(cost.getKey())) {
cheapest = cost.getValue();
cheapestNode = cost.getKey();
}
}
System.out.println("next cheapest: " + cheapestNode);
return cheapestNode;
}
This method is to find the next cheapest node that is not processed yet. Here is the important part:
if (cost.getValue() <= cheapest && !processed.contains(cost.getKey()))
We used a processed list to store the nodes that have been processed in Graph:
private List<String> processed = new ArrayList<>();
After all the nodes are calculated, then all the nodes should be in processed list. Here is the end condition:
if (nodes.size() == processed.size()) // all nodes are processed
return null;
We need to initialize the processed list in Graph like this:
{
processed.add(start);
processed.add(fin);
}
Because start and end nodes will never be calculated and they are already processed. Now let us check the entry function:
public void dijkstra() {
System.out.println("Initial costs: " + costs);
String node = nextCheapestNode();
path.put(node, start);
while (node != null) {
int cost = costs.get(node);
Set<Edge> neighbors = findNeighbors(node);
for (Edge neighbor : neighbors) {
int newCost = cost + neighbor.getWeight();
if (costs.get(neighbor.getTo()) > newCost) {
costs.put(neighbor.getTo(), newCost);
path.put(neighbor.getTo(), neighbor.getFrom());
}
}
processed.add(node);
node = nextCheapestNode();
}
}
This function will find the first node to calculate:
String node = nextCheapestNode();
Then it will enter the calculation loop to calculate all the nodes in graph according to the algorithm:
while (node != null)
In the loop, the function will find the next cheapest node, calculate the path weight, and update the costs table. In additon, it will generate the path:
private Map<String, String> path = new HashMap<>(); // to -> from
The path is the parent data structure in the book, it contains the to -> from data pair. We can use this data structure to generate a complete path from end to start.
Why it’s from end to start? It’s determined by the algorithm calculation process, we may have some orphan paths in above data structure as the result of updated costs calculation, but we can always find a sole path from end to the start.
During the calculation process, if it finds a cheaper path, the from of a to will be updated, so we use to as key and from as value. In this way, where is the to from is always unique, and some to -> from entries will become orphan and useless. But that doesn’t matter, because we get a unique to <- from <- to <- from path. We can clear path data easily. Finally let’s recheck the usage of the codes:
Graph g = new Graph();
g.addEdge("start", "a", 1);
g.addEdge("start", "b", 1);
g.addEdge("a", "b", 1);
g.addEdge("b", "c", 1);
g.addEdge("a", "c", 1);
g.addEdge("c", "fin", 1);
g.addEdge("b", "fin", 1);
The above codes will create this graph:
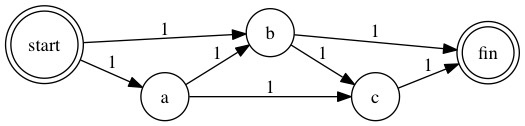
Then we execute the algorithm:
g.dijkstra();
And finally we print out the path:
System.out.println(g.generatePath());
The generatePath() is to print the path from end to start by using path data:
private String generatePath() {
StringBuffer result = new StringBuffer();
String next = null;
for (Map.Entry<String, String> p : path.entrySet()) {
if (p.getKey().equals(fin)) {
result.append(p.getKey()).append(" <- ");
next = p.getValue();
}
}
while (next != null) {
for (Map.Entry<String, String> p : path.entrySet()) {
if (p.getKey().equals(next)) {
result.append(p.getKey()).append(" <- ");
next = p.getValue();
if (next.equals(start)) {
result.append(start);
next = null;
}
}
}
}
return result.toString();
}
It will find the end node firstly, and use it as the initial to, then it will find its from in path data, and do this in a loop and it reaches the start point. Let’s see the result:
Updated cost:fin=2
fin <- b <- start
The cheapest path of above graph is fin <- b <- start. Now let’s try to change the weight of some nodes:
g.addEdge("start", "a", 1);
g.addEdge("start", "b", 10);
g.addEdge("a", "b", 1);
g.addEdge("b", "c", 1);
g.addEdge("a", "c", 1);
g.addEdge("c", "fin", 1);
g.addEdge("b", "fin", 10);
The graph becomes:
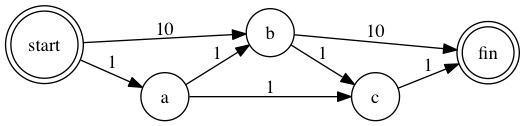
We can see the weight of start -> b and b -> c have been increased. Now let’s rerun the algorithm:
Updated cost:fin=3
fin <- c <- a <- start
We can see the cheapest path has been changed accordingly. Dijkstra’s Algorithm is an interesting algorithm and worth studying.
References
-
Bhargava, Aditya Y.. Grokking Algorithms: An Illustrated Guide for Programmers and Other Curious People. Shelter Island: Manning, 2016. Print. ↩